Second Order Derivative Interpolation - Complex Solution, Simple Problem
While on a quest to increase polish in my game, I began to add animations and camera movements to my UI, which had been static so far. My first step was to tackle the character select screen. I decided to add a camera zoom, movement, and some character card fly-ins.
While this was much more visually appealing than the previous static scene, I had one big problem with it: the zooming. At this point I handled the zooming in a quick and dirty way, increasing the zoom level linearly until it hit the desired level while also shifting the camera to the desired center. This accomplished my task but felt rigid and jumpy.
After searching the internet and the Godot docs for answers, I found many straightforward solutions, namely: Tweens, using the animation player, and using built in functions to interpolate the camera values. I was about to go ahead with this when I found a far more interesting solution: Second Order Derivative Interpolation.
Essentially, treating the zoom level the same as position in a motion equation we can use velocity (the first derivative) and acceleration (the second derivative) to apply some characteristics that inform how we want the motion of the zoom to behave. This approach allows for fine tuning using three parameters: frequency (f), the damping coefficient (z), and the intial response (r). Changing the frequency informs how fast (in hertz) the system oscillates, the damping coefficient determines how the system conforms to the goal, and the initial response determines how quickly the system responds (even allowing for an inverted response). One the right side of the equation we have the control input (x) and its derivative (x'). You can see this represented in the equation below:
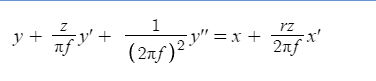
The one problem I encountered was determining how to inform the system to stop such that it would ease in and out at the zoom level I wanted and allow the parameter tuning to do its thing. I knew that controlling this laid with the input variable x but for the life of me I could not figure this out. Luckily my controls engineer friend was able to help me come up with 'yi' and 'yf' which are the initial and final zoom positions. This would allow us to modify the right side of the equation and tune the system to conform to our 'yf' in a predetermined time span. Here is the result:
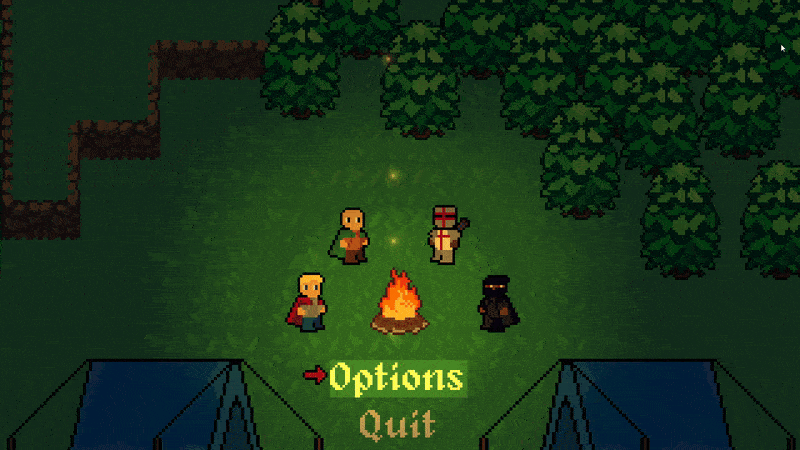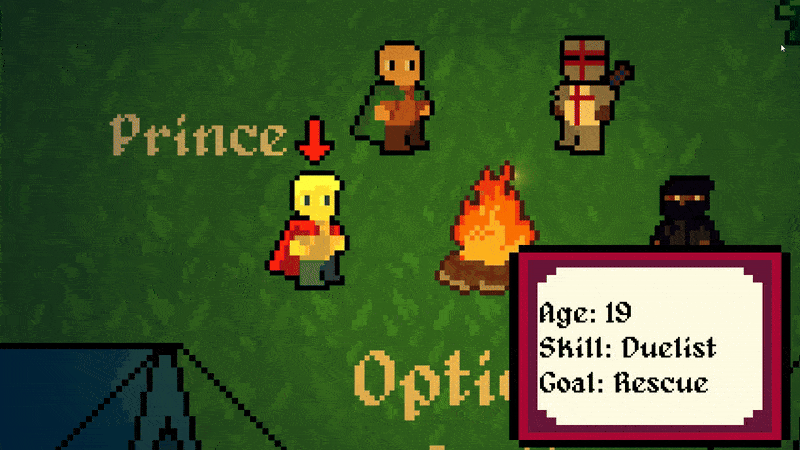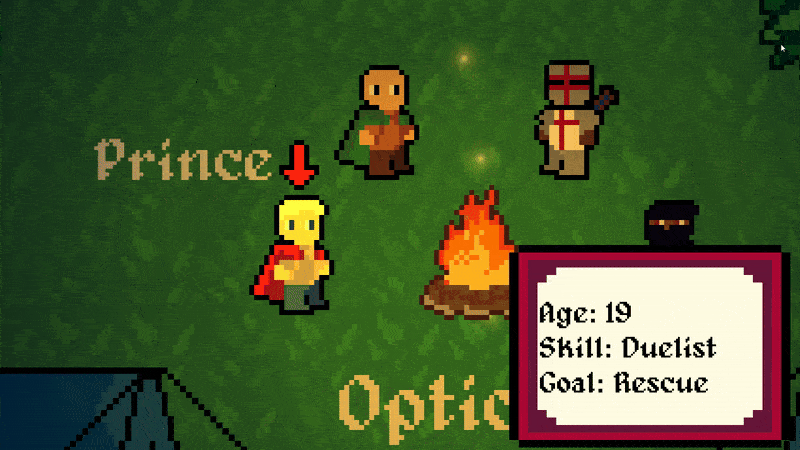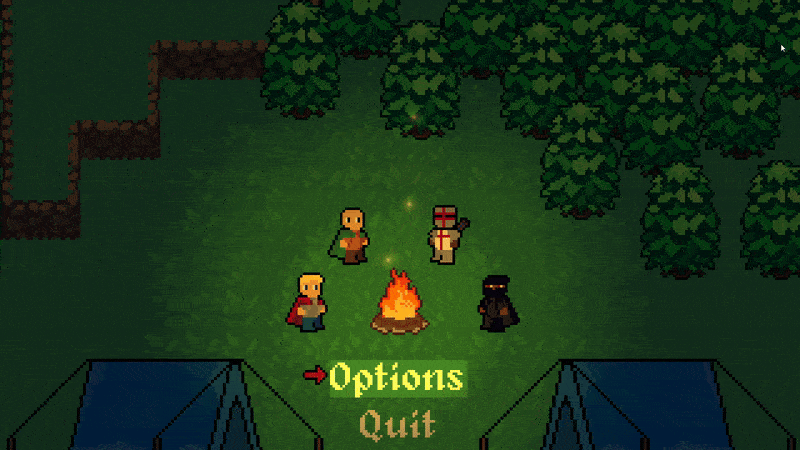
TLDR: I used a naval cannon to kill a mosquito and second order interpolation has many cool uses for creating well tuned animations.
You can also watch a very interesting video about the concept applied to procedural animations here:
Get Blade and Burden Demo
Blade and Burden Demo
| Status | In development |
| Author | Gear Shift studios |
| Genre | Action |
| Tags | 2D, Dungeon Crawler, Pixel Art, Roguelite |
More posts
- Steam Next Fest - A RetrospectiveOct 27, 2024
- New Demo Released!Oct 15, 2024

Leave a comment
Log in with itch.io to leave a comment.